第一章五、弹性碰撞和非弹性碰撞

第1题 (单选题) 难度 - 基础题：

下列关于碰撞的理解正确的是(　　)

A: 碰撞是指相对运动的物体相遇时，在极短时间内它们的运动状态发生了显著变化的过程
B: 在碰撞现象中，一般内力都远大于外力，所以可以认为碰撞时系统的动能守恒
C: 如果碰撞过程中机械能守恒，这样的碰撞叫作非弹性碰撞
D: 微观粒子的相互作用由于不发生直接接触，所以不能称其为碰撞

解析:

碰撞是十分普遍的现象，它是指相对运动的物体相遇时在极短时间内它们的运动状态发生显著变化的过程；一般内力远大于外力，系统动量守恒，动能不一定守恒；如果碰撞中机械能守恒，就叫作弹性碰撞；微观粒子的相互作用同样具有短时间内发生强大内力作用的特点，所以仍然是碰撞，故A正确。

第2题 (单选题) 难度 - 基础题：

甲、乙两人穿着同款充气“防护服”，由于两人初次穿充气服，走路时控制不好平衡，所以两人发生了碰撞。若甲的质量为m，乙的质量为3m，且以相同的速率v在光滑水平面上发生相向碰撞，碰撞后乙静止不动，则这次碰撞(　　)

A: 属于完全非弹性碰撞
B: 属于弹性碰撞
C: 动能损失最多
D: 碰撞后甲的速度大小为v

解析:

设碰撞后甲的速度为v'，以乙的运动方向为正方向，根据动量守恒定律可得3mv－mv＝mv'，故碰后甲的速度为v'＝2v；碰前甲、乙的总动能为E_k＝ $\frac{1}{2}$ ×3mv²+ $\frac{1}{2}$ mv²＝2mv²，碰后甲、乙的总动能为E_k'＝ $\frac{1}{2}$ mv'²＝2mv²，由于碰撞前后总动能相等，所以此碰撞为弹性碰撞，故B正确。

第3题 (多选题) 难度 - 基础题：

(多选)如图甲所示，在光滑水平面上的两个小球发生正碰，小球的质量分别为m₁和m₂，图乙为它们碰撞前后的x－t图像，已知m₁＝0.1 kg，由此可以判断(　　)

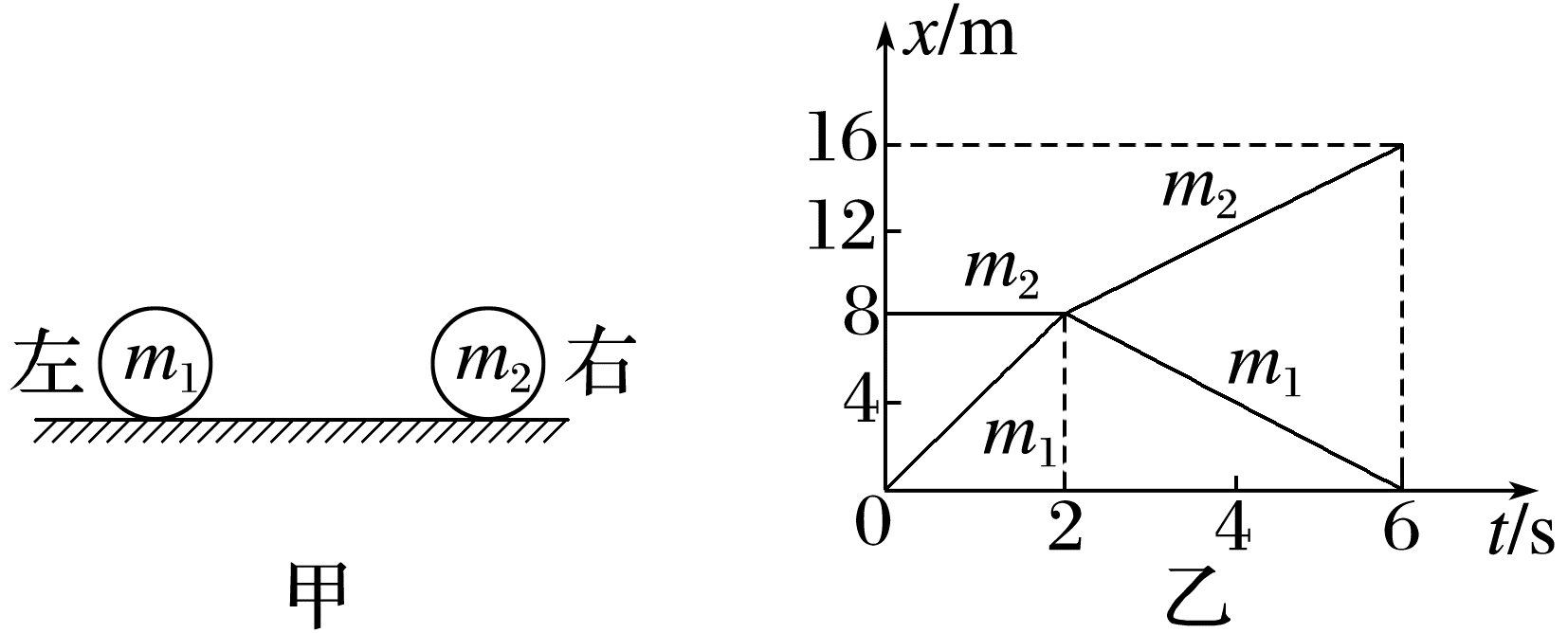
A: 碰前m₂静止，m₁向右运动
B: 碰后m₁和m₂都向右运动
C: 由动量守恒可以算出m₂＝0.4 kg
D: 此碰撞过程为弹性碰撞(机械能没有损失)

解析:

由x－t图像的斜率得到，碰前m₂的位移不随时间而变化，处于静止状态，m₁的速度大小为v₁＝ $\frac{Δ x}{Δ t}$ ＝4 m/s，方向只有向右才能与m₂相撞，故A正确；

由题图可知，碰后m₂的位移变大，说明向右运动，m₁的位移变小，说明向左运动，故B错误；

由题图求出碰后m₂和m₁的速度分别为v₂'＝2 m/s，v₁'＝－2 m/s

根据动量守恒定律得m₁v₁＝m₂v₂'+m₁v₁'，解得m₂＝0.3 kg，故C错误；

碰撞过程中系统损失的机械能为ΔE＝ $\frac{1}{2}$ m₁ ${v_{1}}^{2} － \frac{1}{2}$ m₁v₁'²－ $\frac{1}{2}$ m₂v₂'²，代入数据解得ΔE＝0，故D正确。

第4题 (单选题) 难度 - 基础题：

图甲为冬奥会上中国队员投掷冰壶的镜头，在某次投掷中，冰壶甲运动一段时间后与静止的冰壶乙发生碰撞(图乙)，已知两冰壶质量相等，碰撞可看作弹性正碰，下列四幅图中能表示两冰壶最终位置的是(　　)

解析:

两冰壶碰撞可看作弹性正碰，

则由动量守恒和能量关系可知

mv₀＝mv₁+mv₂， $\frac{1}{2}$ m ${v_{0}}^{2} ＝ \frac{1}{2}$ m ${v_{1}}^{2}$ + $\frac{1}{2}$ m ${v_{2}}^{2}$ ，

解得v₁＝0，v₂＝v₀，即两冰壶交换速度，而后乙做匀减速运动直到停止，则两冰壶最终位置如A所示。

第5题 (单选题) 难度 - 基础题：

(2024·宁波市高二校考)如图，两滑块A、B在光滑水平面上沿同一直线相向运动，滑块A的质量为m，速度为2v₀，方向向右，滑块B的质量为2m，速度大小为v₀，方向向左，两滑块发生弹性碰撞后(　　)

A: A向左运动，速度大小为v₀
B: A向右运动，速度大小为v₀
C: A静止，B也静止
D: A向左运动，速度大小为2v₀

解析:

A、B发生弹性碰撞，取向右为正，

则m·2v₀－2mv₀＝mv_A+2mv_B，

$\frac{1}{2}$ m× $(2 v_{0})^{2}$ + $\frac{1}{2}$ ×2m ${v_{0}}^{2} ＝ \frac{1}{2}$ m ${v_{A}}^{2}$ + $\frac{1}{2}$ ×2m ${v_{B}}^{2}$

解得碰后A的速度为v_A＝ $\frac{m_{A} - m_{B}}{m_{A} + m_{B}}$ ·2v₀+ $\frac{2 m_{B}}{m_{A} + m_{B}}$ (－v₀)，

得v_A＝－2v₀，即A向左运动，速度大小为2v₀，故选D。

第6题 (单选题) 难度 - 基础题：

(2024·乐清市高二质检)如图所示，动量分别为p_A＝6 kg·m/s，p_B＝8 kg·m/s的两个小球A、B在光滑的水平面上沿一直线向右运动，经过一段时间后两球发生正碰，分别用Δp_A、Δp_B表示两小球动量的变化量，则下列选项中可能正确的是(　　)

A: Δp_A＝－2 kg·m/s，Δp_B＝2 kg·m/s
B: Δp_A＝3 kg·m/s，Δp_B＝3 kg·m/s
C: Δp_A＝3 kg·m/s，Δp_B＝－3 kg·m/s
D: Δp_A＝－12 kg·m/s，Δp_B＝12 kg·m/s

解析:

若Δp_A＝－2 kg·m/s，Δp_B＝2 kg·m/s，

遵守动量守恒定律，

碰撞后A、B的动量分别为p_A'＝p_A+Δp_A＝6 kg·m/s+(－2)kg·m/s＝4 kg·m/s，

p_B'＝p_B+Δp_B＝(8+2)kg·m/s＝10 kg·m/s，

A的动量减小，B的动量增加，

则碰后A的动能减小，B的动能增加，

总动能可能不增加，

所以是可能的，故A正确；

若Δp_A＝3 kg·m/s，Δp_B＝3 kg·m/s，

不遵守动量守恒定律，故B错误；

由于碰撞过程中，B受到向右的冲量，B的动量应增加，Δp_B不可能为负数，故C错误；

若Δp_A＝－12 kg·m/s，Δp_B＝12 kg·m/s，

遵守动量守恒定律，

则碰后p_A'＝－6 kg·m/s，p_B'＝20 kg·m/s，

碰后A的动能不变，

B的动能增加，总动能增加，

违反了能量守恒定律，故D错误。

第7题 (单选题) 难度 - 中档题：

如图所示，在光滑的水平面上有2 022个完全相同的小球等间距地排成一条直线，均处于静止状态。现给第一个小球初动能E_k，若小球间的所有碰撞均为对心完全非弹性碰撞，则整个碰撞过程中损失的机械能总量为(　　)

A: $\frac{E_{k}}{2 022}$
B: $\frac{E_{k}}{2 022^{2}}$
C: $\frac{2 021 E_{k}}{2 022}$
D: $\frac{2 021^{2} E_{k}}{2 022^{2}}$

解析:

以第一个小球初速度v₀方向的为正方向，由于小球间的所有碰撞均为对心完全非弹性碰撞，每次碰撞后小球速度都相同，故最后每个小球速度都相同，将2 022个小球组成的整体看作一个系统，设系统最终的速度为v，运用动量守恒定律得mv₀＝2 022mv，解得v＝ $\frac{v_{0}}{2 022}$

则系统损失的机械能为ΔE＝ $\frac{1}{2}$ m ${v_{0}}^{2} － \frac{1}{2}$ ×2 022mv²

而 $\frac{1}{2}$ m ${v_{0}}^{2}$ ＝E_k，解得ΔE＝ $\frac{2 021 E_{k}}{2 022}$ 。故选C。

第8题 (单选题) 难度 - 中档题：

(2024·杭州市高二期末)在冰壶比赛中，某队员利用红壶去碰撞对方的蓝壶，两者在大本营中心发生对心碰撞如图(a)所示，碰撞前、后两壶运动的v－t图线如图(b)中实线所示，其中红壶碰撞前后的图线平行，两冰壶质量相等，则(　　)

A: 两壶发生了弹性碰撞
B: 碰后蓝壶速度为0.8 m/s
C: 碰后蓝壶移动的距离为2.4 m
D: 碰后红壶所受摩擦力小于蓝壶所受摩擦力

解析:

由题图可知，碰前红壶的速度v₀＝1.0 m/s，碰后速度为v₀'＝0.2 m/s，碰后红壶沿原方向运动，设碰后蓝壶的速度为v，取碰撞前红壶的速度方向为正方向，根据动量守恒定律可得mv₀＝mv₀'+mv

代入数据解得v＝0.8 m/s

由于 $\frac{1}{2}$ m ${v_{0}}^{2}$ > $\frac{1}{2}$ mv₀'²+ $\frac{1}{2}$ mv²，碰撞过程机械能有损失，碰撞为非弹性碰撞，A错误，B正确；

根据图线与横轴围成的面积表示位移，可得，碰后蓝壶移动的位移大小x＝ $\frac{v}{2}$ t＝ $\frac{0.8}{2}$ ×5 m＝2 m，C错误；

根据v－t图像的斜率绝对值表示加速度大小，可知碰后红壶的加速度大于蓝壶的加速度，两者的质量相等，由牛顿第二定律可知，碰后红壶所受摩擦力大于蓝壶所受的摩擦力，D错误。

第9题 (多选题) 难度 - 中档题：

(多选)(2024·浙江省高二期中)如图甲所示，“充气碰碰球”游戏是一项很减压的趣味运动项目。为了研究其中的碰撞规律，简化为如图乙所示的模型：直径相同的A球和B球碰撞前后都在同一水平直线上运动，碰前A球的动量p_A＝50 kg·m/s，B球静止，碰后B球的动量变为p_B＝40 kg·m/s。则两球质量m_A与m_B间的关系可能是(　　)

A: m_B＝0.3m_A
B: m_B＝m_A
C: m_B＝1.5m_A
D: m_B＝5m_A

解析:

以A球的初速度方向为正方向，

由碰撞过程系统动量守恒得p_A＝p_A'+p_B，

解得p_A'＝10 kg·m/s

根据碰撞过程总动能不增加，

有 $\frac{{p_{A}}^{2}}{2 m_{A}}$ ≥ $\frac{{p_{A}}^{' 2}}{2 m_{A}}$ + $\frac{{p_{B}}^{2}}{2 m_{B}}$ ，解得m_B≥ $\frac{2}{3}$ m_A

碰后两球同向运动，A的速度不大于B的速度，

则有 $\frac{{p_{A}}^{'}}{m_{A}}$ ≤ $\frac{p_{B}}{m_{B}}$ ，解得m_B≤4m_A

因此，两球质量关系为 $\frac{2}{3}$ m_A≤m_B≤4m_A。故B、C正确，A、D错误。

第10题 (计算题) - 简答题难度 - 中档题：

如图所示，质量M＝5.0 kg的混凝土砌块静止在光滑的水平地面上，质量m＝1.0 kg的小球以v₀＝12 m/s的水平速度向右撞击砌块，碰撞后小球以v＝3 m/s的速度被反向弹回。已知小球与砌块的作用时间为Δt＝0.03 s。

(1)求碰撞后砌块的速度大小；

(2)求小球与砌块碰撞时平均作用力的大小；

(3)若砌块左侧涂上胶水，使小球与砌块碰后粘在一起，求碰撞过程系统损失的机械能。

答案:

(1)3 m/s　(2)500 N　(3)60 J

解析:

(1)设砌块碰撞后的速度为v₁，

规定水平向右为正方向，

由动量守恒定律得mv₀＝m(－v)+Mv₁，解得v₁＝3 m/s

碰撞后砌块的速度大小为3 m/s。

(2)设碰撞时平均作用力大小为F，规定向右为正方向，

对砌块由动量定理得FΔt＝Mv₁－0，解得F＝500 N，

小球与砌块碰撞时平均作用力的大小为500 N。

(3)设碰后两者共同速度为v₂，规定向右为正方向，

由动量守恒定律得mv₀＝(m+M)v₂，解得v₂＝2 m/s

设碰撞过程损失的机械能ΔE，

根据能量守恒定律有

ΔE＝ $\frac{1}{2}$ m ${v_{0}}^{2} － \frac{1}{2}$ (m+M) ${v_{2}}^{2}$ ，解得ΔE＝60 J

碰撞中系统损失的机械能为60 J。

第一章 五、弹性碰撞和非弹性碰撞

第一章五、弹性碰撞和非弹性碰撞